최근 도전하는 문제들 중에 되게 좋은 문제라 생각돼서 소개해본다.
문제: 링크(프로젝트 오일러)
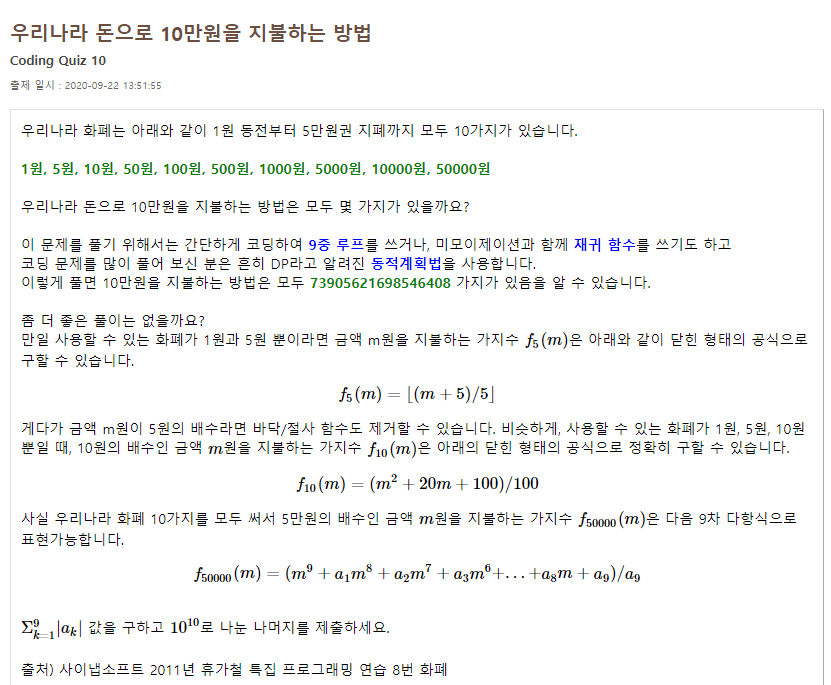
다른 문제들은 어찌저찌 풀었는데, 얘는 골때린다. 도대체 해결한 사람들은 어떻게한거지 ㅋㅋ
계수의 합을 구하는 것이기 때문에 수식구하고 m=1 때려주고 a_9 곱해주면 되는건데 젠젠 모르겠다.
첫번째 접근 수학적 귀납법
규칙성이 있다고 가정하고, 말도안되지만 귀납적 추론으로 아래 와 같은 공식으로 생각하여 값을 넣었다.

당연히 틀림 ㅋㅋ
두번째 접근 연립방정식 미지수 9개
미지수 9개면 9개 수식이 필요하다. 즉 9개의 정답이 필요한데...
1개는 이미 나와있다고 치고.. 남은 8개를 구하는데 이미 그 수가 상식을 뛰어 넘을 수 이기 때문에 아마 다른 접근 방식이 필요하다.
세번째 접근 규칙성 찾기
할 수 있는대로 1,5,10,50 에 대한 수식을 구했다. 맞는지 틀렸는지 모르겠지만.

인수분해 해봤고

인수분해 결과로 봤듯 50을 제외한 숫자는 연관성이 떨어져보인다. 즉 큰 연관성이 없다고 생각된다.
그렇지만 1 과 5의 관계는 5배이지만 5와 10의 관계는 2배이라는 점으로 보아 아마 1->5로 갈 때의 규칙과 5->10으로 갈 때의 규칙이 다를 것으로 예상된다.
수기로 계산할 때 계차수열의 합이 어렴풋 보였다. 시그마의 시그마의 시그마의... 이런식으로 계산되는 것 같음 -> 적분인가...
일반적으로 알고리즘은 점화식이고 점화식만 알게 된다면 구현할 수 있을 건데, 잘모르겠다.
지금도 1~100까지로 범위 확장해서 수식 계산중인데, 이게 맞나 싶으면서 하고 있다..
오랜만에 수학공부하고 공식 찾고 유도하는게 재밌긴한데 아예 감이 잡히질 않는다...
재밌어서 그냥 한번 소개해봤다. 이상..
'개발일지 > 알고리즘-문제풀기' 카테고리의 다른 글
| 프로그래머스 - LV1 - 체육복 (1) | 2023.12.20 |
|---|---|
| 프로그래머스 - LV1 - 신규 아이디 추천 (0) | 2023.12.19 |
| 프로그래머스 - LV1 - 기사단원의 무기 (2) | 2023.12.07 |